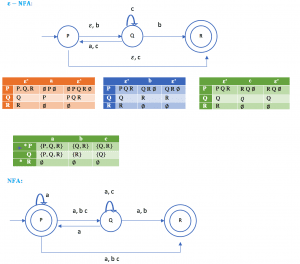
Example of Conversion of Epsilon ε-NFA to NFA – 3
Example 3: Convert the following ε-NFA to its equivalent NFA
Example 3: Convert the following ε-NFA to its equivalent NFA

Example : Convert the following ε-NFA to its equivalent NFA
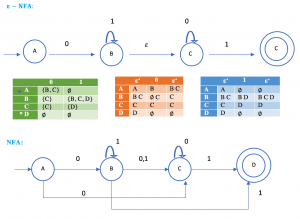
Example : Convert the following ε-NFA to its equivalent NFA
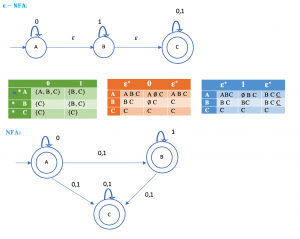
Minimization of DFA (Table Filling Method or Myhill-Nerode Theorem)
Steps:
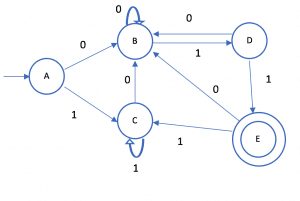
Example: Minimize the following DFA using Table Filling Method.
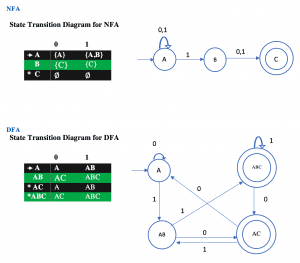
Example : Design a NFA for a language that accepts all string over {0,1}, in which the second last symbol is always 1. Then convert it to its equivalent DFA.
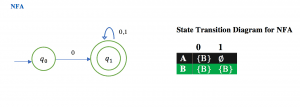
Example :Given below is the NFA for a language L= {Set of all string over (0, 1) that ends with 01 } construct its equivalent DFA.
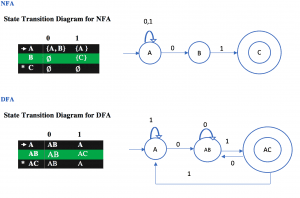
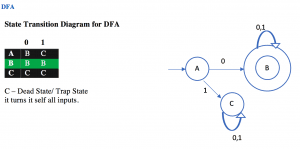
Example: Find the equivalent DFA for the given by M= [{A, B, C}, (a, b), , A, {C}] where δ is given by:
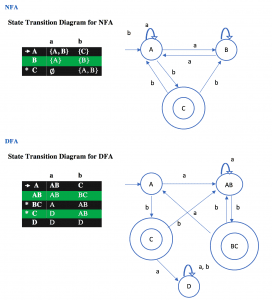
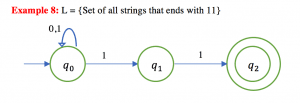
Example : L = {Set of all string over (0,1) that ends with 1}
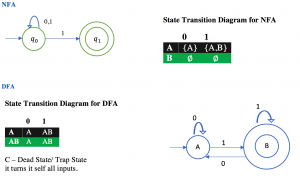
Example: L= {Set of all strings over (0,1) that start with 0}